- 小学校６年生の夏休み自由研究（親の視点で）- 振り子の等時性の破れ

これまで，
- 小学校３年生の夏休み自由研究（親の視点で）-
- 小学校４年生の夏休み自由研究（親の視点で）-
でセミの研究での（親と子の^^）奮闘について執筆してきた．
５年生では学校で習った円周率を理科的な課題にして，
- 小学校5年生の夏休み自由研究（親の視点で）-
のように与えてみたのだが，先生が「理科的」とはみてくれず，コンテストに出してくれなかったと悔しがっていた（笑）．

そこで，小学校自由研究としての最後となる６年生としては「100%理科^^;」で行きたいらしかった．候補としては水溶液で何かやりたい，，，などあれこれ考えていたが，（親の目からみると）なかなか見通しが立てられていない．もちろんそれはそれでいい，という考え方もある．

＜小学校で習うこと＞
　ちょうど，５年生の終わり頃に学校で振り子について習ったようだ．振り子の周期は弦の長さでかわり，質量や振幅にはよらない．いわゆる「振り子の等時性」である．

　大学以上の物理では，この振り子の等時性は小振幅のときの近似であることを学ぶが，これについては，時々インターネットで話題になる．小学校の実験で等時性の破れが見出されたとき，それをどう生徒につたえるか，ということが論点に思える．

　そこで，「小学校では周期は振れ幅によらない，と習うが，理系の大学生以上なら，実はちょっとだけ変わるってことを知ってる．証明してみる？」とけしかけた（笑）．自分でも水溶液実験をどう組み立てるか決めかねてたようすで，だんだんその気になってきた（笑）．

＜小学校の教科書＞
　小学校教科書（大日本図書）ではどのように習っているのか見せてもらったら，
1) 予備実験をさせる．
2) その結果周期の違いの原因は「振れ幅」「長さ」「重さ」があり得ると提起．
3) 本実験
　実験１：　振れ幅15°と30°を比べる
　実験２： 長さを 100, 25, 50 cmで比べる　
　実験３: 金属の玉，木製の玉，ガラス玉で比べる
となっている．
　測定方法はストップウォッチを用いて１０往復を５回測って平均をとるように指示されている（これでは残念ながら精度がでない）．

4) 実験の結果，下図のように結果が与えられている（やや不満．．）

　[引用元：大日本図書 小学校５年生理科 p.67]

5) 資料としてガリレオの「振り子の等時性」発見にかかわる逸話が掲載されている
　（人物を関連させるのは記憶の定着にも一般教養にもよい）
6) 手作りのメトロノーム　（いい工夫）
7) 発展編：連成振り子 （なかなか高度だ）
8) ふりかえり．

＜文科省　小学校学習指導要領解説 (web)　＞
小学校学習指導要領解説　理科(pdf)（平成20年6月）の該当箇所をみると，
p.55
　「ここでの指導に当たっては,糸の長さや振れ幅を一定にしておもりの重さを変えるなど,変える条件と変えない条件を制御して実験を行うことによって,実験結果を適切に処理し,考察することができるようにする。その際,適切な振れ幅で実験を行い, 振れ幅が極端に大きくならないようにする。また,伸びの少ない糸を用い,糸の長さ は糸をつるした位置からおもりの重心までであることに留意する。さらに,実験を複 数回行い,その結果を処理する際には,算数科の学習と関連付けて適切に処理するようにする。」

との記載があり，大振幅は想定していない（させない）ように読み取れる．

＜問題点＞
（１） ひとつの問題は，児童が自主的に大振幅で行った場合にどう対処するか，ということであろう．
仮に先生から，「あまり大きく振らないように」と指示されたとすると，
--- 言われた通りに従う　→　　我が子はこっちかな？
　から
--- 隙を見て大振幅でやってみる　→　私は絶対こっち（笑）
　まで，子供の対応は様々だと思う．

（２）もうひとつの問題は小数点をどこまで扱うか，というところである．
幸い，平成１０年改訂版（旧課程算数）→平成２０年改訂版（新課程算数）

の改訂で，円周率が「3.14,目的に応じて3と配慮」→　「3.14」（へ戻った？）ことが話題となったが，むしろ小数の計算の
「1/10の位までの小数の計算(5年)」
→「３年で1/10の位，4年で1/100の位以下の小数点（計算は1/100まで）」
の改訂が重要であろう．なぜなら，振り子の実験で必要な精度は1/100の桁以下に現れるからである．


実際，振り子の等時性を実験的に見出すことはさほど難しくはないが，小学校となると測定精度や再現性の問題が浮上する．


＜参考：教育専門家の意見＞
[参：塩野正明・松村敬治「小学校理科における「振り子の運動」の 実験指導と誤差の扱いについて」西南学院大学人間科学論集 第7巻 第1号 107 - 121 頁 2011年8月]

では，学習指導要領の平成１０年改訂版（旧課程）と平成２０年改訂版（新課程：現行）では，扱える誤差の桁がかわってくるとの指摘がなされている．

=======================自由研究内容===================
さて，本題に入ろう．．．．．．．

＜実施の準備＞
さて，６年生ともなると，親の負担（笑）はずいぶん減ってきた．ただし，資材調達については子供では無理なので，ホームセンターに行って物色する（親も装置を思案しながら探すのだが，これが実は楽しい・・・笑）．

ポイントは２つ
- 測定精度を上げるため，長寿命の振り子を作ること
- 大振幅に限定して測れるようにすること
これについては，誘導尋問をしながら，必要性を理解させた（つもりだが，，，，）

長寿命の振り子は，いろいろな方法があると思うが，"普通の"小学生の工作としては敷居が高い．そこで，長さ，材質，重さを変えて長寿命となる条件を洗い出す方針とした．

装置は，角度を正確に測ろうとすると，分度器を設置するには，中心の精度や振り子平面の回転で100周期程度自由に触れ続けるようにするのは難儀である．そこで，立体感覚のトレーニングにもなるかと思い．角度を測った糸を空中に２ヶ所張り，両者が重なってみえるように移動することで，２つの糸がつくる平面上に，目と振り子の初期位置を合わせる方法を提案した．廊下を糸だらけにして，なんとなく楽しそう（？）であった．角度の測定には建築現場で梁などの角度測定に用いる工具を採用した．

＜実験方法＞
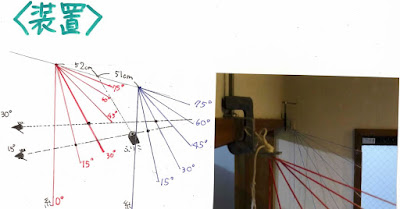
測定方法
1- ストップウォッチについては，スマートフォンのラップ機能付きを用いた．100周期測ればかなり正確になるのだが，数え間違いを防ぐために，ラップが役に立つ．

2- 研究としては，さらに一工夫必要だろう（と親は考える^^）．そこで，教科書のメトロノームの発想だが，より精度を上げるため，デジタルのメトロノームで周期をチューニングする手法を提案した．










＜実験１＞
- 分銅（インターネットでそこそこの精度のものが安く買える）を使って，重い方が寿命が長い
- ワイヤーロープのほうが糸よりも寿命が長い
ことが見出された

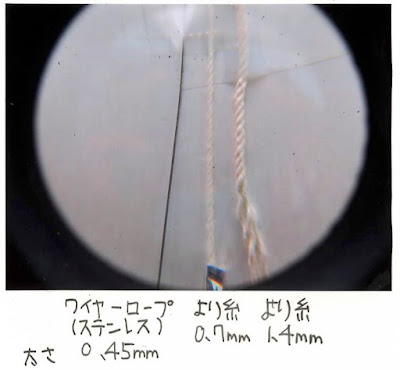
こうして，ワイヤーロープを使い，重さ100gの分銅

＜実験２＞
- 長さと周期についてメトロノームで精度よく測れることを示す．長寿命の振り子が役に立つ．

解析
- やや小学生には高度すぎるが，周期を２乗したものでもグラフをつくってみるようにやらせてみた．


結果はかなりいい感じであった．実験２で，長い振り子の場合にメトロノームの誤差が大きかったが，これは手法が不慣れであったのと，テンポが遅いときのチューニング精度によるところが多いだろう．これには2倍速，4倍速でチューニングすればよかったであろう（本人の理解次第）．

縦軸の単位の間違い（正しくは秒^2 ）に気づいたのは，コンテストから返却されてきた後だった．最初は意味がわからない様子で怪訝な表情であったが，「面積の単位はmの2乗と書くだろう？」というと，ハッと青ざめていた．いい教訓になったであろうか（親の思惑^^）．

比例の計算は習っているので，関係式　周期(秒)x周期（秒） = 0.41 x L [cm] と求めた．（--- 実は係数１桁間違ってて，正しくは0.041)．小学校の基礎学力（計算力と検算力）大事ですね（笑）．）

さて，肝心の振り子の等時性の破れはどのようになっただろうか．

＜実験３＞

- 振れ幅の依存性．これにはメトロノームが本領発揮．長寿命振り子でも，時間とともに振幅がだんだん小さくので，大振幅に限定することができない．しかし大振幅振り子にメトロノームのテンポをあわせる操作により，何度も振り直しが可能である．

結果を示す．
　

5%程度の「等時性の破れ」が確認された．ただし，子供はそれを「誤差」と表現している（近似値からの逸脱の概念はまだ難しい）．

 図のエラーバーについて，縦はメトロノームの読み取り0.5をプラスマイナスしたときの周期，横は測定中の振幅の変化（概ね15°）を考慮してはどうかと促した．
奮闘の甲斐あってか，コンテストに出してもらい，おまけに賞をもらうことができた．
（昨年の雪辱を少しは果たせたことだろう；笑）

余談だが，学校の先生に「（違いは）測定誤差の範囲だ」と言われたらしく，怪訝な様子であったが，データの信頼性を主張するほどの甲斐性はないようだ。先生は賞をもらったことにビックリされただろうか(^^)．

ご興味のある方のために，全24ページPDF(724kB)を掲載． [http://bit.ly/2jj0fHA ]

展示されている作品を見に行ったが，入賞しているものは，かなりの力作揃いであった．
本作品について，厳しいことを言えば，
- タイトルをもっと工夫をすべき．（提出前に言ってみたものの聞く耳もたず；笑）
- グラフが鉛筆書きで薄くて見にくい（視覚に訴える重要性を実感してないようす）．
- 感想部分の記述がいまいち（苦手意識が強く，筆が進まない様子．．．）．

など，まだまだ改善の余地はあるだろう．
（夏休み最終日に夜中までかかってやるから．．．．．笑）

====================ここからは補足======================

＜大人の解析＞
周期 T = 2π sqrt(L/g)なので， グラフから求めた 比例係数0.041 (SI単位なら4.1) から計算すると　4.1 = 4π^2/g より，重力加速度g = 9.6を得る．

　値としては，やや不満（笑）なので，娘が測定したデータを数値でもらって，直線からずれた部分を除いて直線フィットし，重力加速度gを求めてみた．

結果
　　y = a + bx
a = 0.075332 +/-  0.0386
  b = 0.040317 +/-  0.000518
これより，g = 9.792 ± 0.005 m/s^2 であった，真値は9.80665.. m/s^2なので，かなりの精度ではないだろうか．
    x切片は - 1.87 +/- 0.27  cm　(エラーはΔ(b/a)から出せる)
分銅の中心から測ったので，重心の取り方は考慮したつもり．もしかすると上部の固定部分の軸が少しぶれていたのかもしれない（実効的に糸が長くなる；推測）．もちろんこういった解析は小学校自由研究の範囲外．高校生くらいでパソコンつかってやってみると面白いだろう．

次に等時性の破れについて，理論曲線と測定値を比較した．


実験値は15°のときの値に対する比である。実験値は理論値（同じく15°で規格化；緑実線）ほどの値が得られていないことがわかる（２倍程度違う）．実は実験中，もう少し差がでるのでは，，，と感覚的に思いながら手伝っていた．ズレを認識できたのは37.5°(45°スタートで，30-45°の範囲の値としている）なので，その理論値との比をとっても本質的な差（依存性）は埋まらない．これについては私にとっても今後の課題となった．．．

理論式の楕円積分の近似計算については数値計算サイト
　　http://www1.bbiq.jp/math7557/Elliptic-Integral.html
などでも確認できる．

＜総括＞
　小学校の実験では15°と30°であったようなので，この実験とは矛盾しないらしい（娘談）．しかし，大振幅で精度良い計測を行えば，小学生でも十分に等時性の破れは観察できる．
「振れ幅を変えても１往復にかかる時間はほぼ等しいが，振れ幅が大きくなると，わずかではあるが１往復にかかる時間は長くなる．工夫をして精度いい実験にチャレンジしてみよう！」
　と一文入れてもいいのかもしれない（試験では「ほぼ」を入れること．．かな？）．

(覚書：自由研究は2015.8， 本ブログ作成は2015年末ぐらい，途中でずっと放っておいて，2017.1.15 にようやく推敲して公開)

- 小学校５年生の夏休み自由研究（親の視点で）- 円周率

これまで，

- 小学校３年生の夏休み自由研究（親の視点で）- 

- 小学校４年生の夏休み自由研究（親の視点で）- 

でセミの研究での（親と子の^^）奮闘について執筆してきた．今年は５年生．さて何を選ぼうか（選ばせようか），夏が近づくにつれ，気になっていった．

理科では現在どんなことを習っているのだろうかと思い，学習指導要領を見ると，「植物，動物の誕生，日本の天気，水溶液，電磁力．．」のような内容．この中から選べないかと思ったが，いまいちいい発想が浮かばない．娘も決めかねている．そこで，少し視野を広げて，５年生算数で習う「円周率」を理科的なテーマにできないかな〜と思い立った．

ふと思いたち，物理定数実測の入門演習としての円周率測定として，娘に提案したら，3.14...と学校か学童クラブかで聞いて知っている様子で，食いついてきた（テーマ確定；笑）
しかし，提案してみたものの，どうやれば（やらせれば^^）いいか，研究課題にするのはけっこう難儀である。

まず第一に，円周率測定の意義を伝えるのが大変だ．「円周率とは？」と聞いても「約3」とか「3.14ナントカ」としか帰ってこない（笑）．

そこで，ワークシートを作成し，それに沿って演習を行い，その結果をレポートにまとめるような方針とした．

参考までに，ワークシートの内容を掲載する．ただし実際に用いたものから，いくつかの反省点を考慮して改訂してある（原版はかなり荒削りのまま走った．．）．

==========================================

「円周率をもとめよう」ワークシート：小学生用概要
　　　　（フルバージョンは文末のPDF,Word形式で提供）：

§1 背景

（１）円周率とはなんのこと？

（２）なぜ重要か

（３）歴史

（４）小学生でもわかる複数の方法で，円周率を実測し，単に3.14という数字に留まらない，円周率の姿を体験してもらいたい．
　　必要な材料（本作業で採用した材料）

§２  小学生でもできる方法で円周率をもとめてみる．

（１） アルキメデスのはさみうちを体験してみましょう．

（２）長さを使う．（バビロニアの人たちがやっていた方法の現代小学生版）

（３）面積を使う．

（４）体積を使う．

§３  まとめ

　円周率を精度良く求めるのがかなり大変だ，ということがわかったでしょう．人類はいろいろな方法で円周率を求めてきました．今何桁までわかっているでしょうね．　　　　

                                                                         おしまい

　　　　　　　　　　　　　　　　　　　　　（2014.8起案：S. Kado）

==========================================

物理定数の計測，という観点では，単に算数にでてくる3.14ではなく，未知の定数をどうやって探り当て，精度良く決定するか，という一般科学，物理学の研究にも近いといえるでしょう．私自身，作ってみて，様々な計量，および作図，図表整理，平均や誤差計算など，科学的な思考力と手法を学ぶよいトレーニング教材になったのではないか，と思っています．

自由に活用いただければ幸いですが，どこかに公表される場合は以下を参考に願います．

   講演スライド等：「(c) S. Kado, 2014」

   印刷物・Web： http://plasmankado.blogspot.com/2015/02/circularconst.html

ダウンロード：フルバージョン [ PDF( 200kB),  Word (2011 MAC, 128 kB)  ]   

 （改編は自由ですが，その場合は必ず文中に引用願います）．

例）「  S. Kado, 2014 より許可を得て改編，URL:  http://plasmankado.blogspot.com/2015/02/circularconst.html  」

===========

＜実践＞
　このワークシートをやった後，レポートにまとめさせた．例年のように，A3のケント紙を重ねて本を閉じるように中央で折り，A4の冊子にした．
自由研究　提出版スキャンPDF (1.3MB)：　scanned report

　レポート中，変数がCとかSとか，小学生らしからぬ（笑）ものがでてくる．これは親（＝私）がワークシートを考案する過程で使ったものをそのまま残しておいたことに引きづられている（わざわざ△などに置き換える余力が（親に）なかったし，まあいいか，と．．．）．

　記述力はまだまだだが（誤字もある），ようやく自分で手を動かして作業をするようになってきたように思う．もちろん，測定装置（ノギス，天秤など）の使い方を教えたり，校正（本来は較正の字が適切），実際に測定したりする場合には，横について指示を与える必要はあった．

余談１：これら，データやグラフをまとめるのは，まだ相当時間がかかる．我が地域は夏休みが短いので，またまた提出前の２日間，深夜までかかっての詰め込みであった（最大の責任は取りかかりが遅いこと：笑）．写真は夜中に父親（＝私）が近所のコンビニエンスストアに駆け込み，デジカメプリントをやってくるハメになった．．（大きさ調整のために何度も往復した．．．^^;;）--- パソコンからの印刷はやらない方針（子どもが自力でできないから，という理由 --- だが，深夜のコンビニプリントは自力でできるのか，言われると。。。。^^）
　一部，マジックの清書がまにあわず，鉛筆書きのままのところが残っているのが悔やまれる．．．．

余談２：がんばって仕上げて学校に提出したのだが，数日後，なぜか不満げな様子で帰ってきた．
聞けば，理科自由研究については，コンテストに応募することができたようで，それを希望したようなのだが，「円周率は理科ではない」とう理由で応募が認められなかったとのことだ．「次は誰から見ても理科に見えるものをやる！」と宣言していた（笑）．

（これを明らかな理科演習にするにはどうすればいいだろうか？　ビー玉の選別をビリヤード方式で行うとか..... 　運動量保存則......        もちろん実際は無理だけど；笑）

後日談：５年生の２月になって，算数で円周率がでてきたらしい．厚紙の円を転がして演習を測定する方法が記載されている（厚紙や目盛が教科書の付録になっていて，至れり尽くせりである^^; ）．
　先生に言われて（かな？）夏休みにやったこの課題を学校に持っていき，クラスメイトと「どういうこと〜なるほど〜」などと言い合って見直しているとのこと．先生も一度家に持って帰ってちゃんと（笑）読んで，クラスメイトに説明してくれているようだ，とのこと（真偽は不明^^）．
　夏に「理科の自由研究として」コンテストに出展できなかった悔しさも少しは紛れたのではないだろうか．これもまあいい人生経験になっていると信じたい．


　　　　　　　　　                   　　　　（2015.2. 23         文責　plasmankado ）

理科教科書における光スペクトル再定義の必要性（白熱灯・蛍光灯・LEDを理解する）

本稿は日本物理学会第70回年次大会（2015.3.21-24,早稲田大学）にて登壇する
「理科教科書における光スペクトル再定義の提案」(24aCK-4) に基づくものである．
日本物理学会は執筆者自身の論文については，無条件に再利用することが認められている（日本物理学会誌投稿規定(PDF), （別表）JPSJ・会誌・大会概要集・大学の物理教育 掲載論文 利用許諾基準）ので，ここに全文を紹介する．講演概要はA4 1ページの制限があるので，詳細を追記する．

はたして，「実に興味深い講演概要」になっているだろうか．．．参考(講演概要の書き方PDF) 
====================================
講演概要：
　光のスペクトルは光の波長，原子構造などに関連し，中高の学習指導要領においても重要な概念として位置づけられている．実際，現行新課程の高校学習指導要領解説（理科編, 2009.3）には「科学と人間生活」「物理」「地学基礎」「地学」で計23ヶ所「スペクトル」という語句がある．簡易分光器が科学啓発プログラムで手軽に利用されるようになり，今や一部の教科書の付録に採択されるなど，生徒にとってもさらに親しみやすい題材となっている．
　かねてより教科書でスペクトルは連続スペクトル（熱放射）と線スペクトル（輝線・暗線）に分類されている．ところが，例えば節電対策やノーベル賞受賞で一躍知名度が上がった発光ダイオード(LED)のスペクトルを説明する場合，この分類では窮することがないだろうか．
　現在商用化されている白色LED照明はRGB３原色のLEDを用いているのではなく，青色のLEDと黄色の蛍光体を用いて，擬似的な白色光を実現している．青色成分を相対的に抑えた擬似電球色LEDと併用し，点滅のデューティサイクルを制御することで，両者の中間的な色の変化も可能となるなど，その技術革新は目覚ましい．
　LEDのスペクトルは伝導帯下端の電子分布幅と価電子帯上端の正孔分布幅によって数十nm程度の幅をもつ緩い山なりのスペクトルとなる．さらに蛍光体のスペクトルは，特定の色付近に100 nm以上にわたりなだらかな広がりをもつ．すなわち，これらは連続と言うには細く，熱放射とも無関係で，かといって輝線と言うには広すぎるスペクトル幅を持つ（図参照）．蛍光灯・プラズマテレビからLEDや有機ELにかわりつつある日常生活において，従来のスペクトル分類では不十分かつ不自然であるとの印象がますます強くなってきた．

白色LED測定値とプランクの輻射式    

　熱放射に対し，冷光（蛍光と燐光）の用語もごく稀に目にするが，必ずしも定着していない．科学技術や工業製品，日常生活の現場で使われている用語に科学的に親しむのが理科教育の主眼でもあるので，むしろ「ルミネッセンス」のまま既存の分類を拡張するほうがよさそうである．この用語に従うと，白色ＬＥＤは青色の電子ルミネッセンスと黄色の光ルミネッセンスが合わさったもの，蛍光灯は水銀プラズマの発する輝線スペクトルと白色の光ルミネッセンススペクトルが合わさったもの，と統一的に説明できる．実際，有機EL（エレクトロルミネッセンスと記載）を紹介する新課程中学教科書もある．本分類であれば高校理科で自然に拡張して発光原理とスペクトル形状を説明することが可能であろう．中学以下であれば回折格子を介して観測される印象から，
       とびとび（輝線），
       べったり（熱放射）に加え，仮に
       "もあもあスペクトル"
と称するのはどうであろうか[1]．
 以上の観点から著者は，
　(i)温度を反映し高温の物質が発する連続スペクトル，
　(ii)原子構造を反映し，気体やプラズマが放出・吸収する線スペクトル，
　(iii)半導体や蛍光体が何らかの刺激（電界や光）をうけて間接的に発するルミネッセンススペクトル
に分類を拡張することを提案する．

[1]門信一郎「理科教育の現場にプラズマ・核融合を」プラズマ・核融合学会誌 Vol. 91 No. 2 (2015) pp. 99-106. (PDF 745 kB)
==================================================


＜立ち位置＞
この提案は，あくまで理科教科書内容についてのものです．
厳密な言い方をすると，スペクトル形状に関して分類すると，
「連続スペクトル」には
　- 熱放射：黒体輻射，プランクの輻射式
　- 制動放射：自由電子ー自由電子遷移
　- サイクロトロン（シンクロトロン）放射
　- プラズマの再結合放射：長波長側に「崖」をもつ片側連続のスペクトル
があります．ただし，教科書ででてくるのは，熱放射の部分のみです．

「輝線スペクトル」は，プラズマ中の原子や不完全電離イオンの束縛電子が電子や光子の衝突によって励起遷移し，有限の時定数で起こる発光を伴う脱励起遷移（自然放出）のスペクトルです．波長は脱励起遷移のエネルギー差できまります．この点で，発光ダイオード(LED)の発光過程も類似しています．

一方，発光原理に着目すると，
  i) 熱放射，
  ii) 加速度運動する荷電粒子からの電磁放射，および
  iii) 励起発光
の３分類になるかと思います．
　制動放射やサイクロトロン放射はii)，プラズマ中の原子やイオンが発する輝線やLEDはiii)に含まれます．

では，プラズマからの発光とLEDどちらも輝線スペクトルに含めるのがいいのでしょうか？

　もちろん，それも一理あるのですが，副作用があるのです．どこかを無理に整理しようとすると，別のどこかに齟齬がでてしまう．よくあることですね．

(1) 簡易分光器での観察結果の説明に窮するのではないかと想像します．
　現行の学習指導要領では簡易分光器を作成して実際にスペクトルを観察することが推奨されています．しかし，教材として自作できる分光器では，蛍光灯とLEDランプはまったく違ったスペクトルに見えます．それに加え，真空放電（気体放電），発光ダイオードを別々に学ぶので，それらを混乱させないように組み込むことが肝要だと思います．

(2) 熱放射は星の温度と関連して，小学生でもかなり定着していると思われます．LEDのスペクトルは簡易分光器で見ると，どちらかというと，こちらに近く見えます．すると，色と温度の関係に混乱を引き起こしてしまうことが懸念されます．

＜考察＞
我々科学者は，より一般化，一般化と進みますが，学習者にとって，それは必ずしも最適な道筋とは限らないと思います．まずは性質の区別をしっかり把握し，その後に原理の共通点へと深めていくほうがよいでしょう．
　例えば，硬貨の材料
　　-    1円　　アルミニウム
　　-    5円　　黄銅
　　-  10円 　 青銅
　　- 100円　白銅
　　- 500円　ニッケル黄銅
と説明されると，ある人はこれで納得するでしょうし，さらに，「黄銅とは銅と亜鉛の合金で，いわゆる真鍮」と理解し，さらに「それぞれ何％含有しているかで性質がかわる」と必要に応じて細部に進んでいける．
　もし最初から「500円硬貨は銅72%，亜鉛20%，ニッケル8%」と説明されると，ある人には拒否反応がおきるばかりか，合金ではなく混合物と誤解される懸念もでてきます．
　すなわち，浅くおおまかな分類から細部の原理まで矛盾なく深めていける定義が望ましいと考えます．

　この観点で，LEDの発光を従来的な理科にどのように入れるか，ということに注意が必要だと思うのです．現状いわば，「銅」を学ばずに「黄銅」や「青銅」を学んで終わっているような印象です．
　そこで，中学高校では，
　スペクトルの様子　（べったり，とびとび，もあもあ），に始まり，
　スペクトルの性質　
　　    - 熱放射（連続スペクトル，温度に依存），
　　　- 輝線スペクトル（細い，エネルギー準位に依存），
　　　- ルミネッセンススペクトル（線幅や形状が物質により様々，輝線に類似）
と分類し，自然界や光製品の様々な発光を説明できるようになり，大学に進学するに従いスペクトル生成の原理：
　　　- 加速度運動する荷電粒子の電磁放射
　　　- 原子の輝線と半導体の再結合発光の詳細な原理
　　　　（広義のルミネッセンス，蛍光や燐光），
　　　- プラズマの再結合放射は半連続（長波長側に崖をもつ）になること，
　などを学んでいけばよいのではないかと思います．

  　　 2015.3.20 公開（ブログは未完成ですが講演間近なので公開：図なども入れたい）

　　              　　　　　　　　　　　　　　　（文責　@plasmankado）

===================
3/24 追記：講演を終えました．フロアからの質問があったので，記載します．

Q 　　　帯スペクトル（バンドスペクトル）というのはどうか．
　　ルミネッセンスは形状のことを指すのではなく，プロセスのことを指している．
A    　もっともなご意見だと思いました．実際，帯状スペクトルの名称はどうだろうか，と悩んだこともありました．いまだ，結論がでているわけではないのですが．以下のように考えます．
　バンドスペクトルは，分光学の用語では，分子の振動，回転構造を指します．例えば，プラズマ中の水素分子(Werner-band, Lyman-band, Fulcher-band)，窒素分子(1st positive, 2nd positive etc), HCl, CHラジカル，C2ラジカル（C2 スワンバンド）など，かなり有名なものがあります．これらは，一見帯状に見えますが，分解能のよい分光器で測定すると，輝線の集合からできていることがわかります．発光過程は，原子の輝線とまったく同じく，電子衝突励起や光衝突励起，解離励起などです．これらの確立された領域にはあまり踏み込みたくないと私は思っています．
  (   核融合境界層プラズマの分子分光   ~可視領域の水素分子スペクトル~ 　PDF
     プラズマ・核融合学会誌  J. Plasma Fusion Res. Vol.80, No.9 (2004)749‐756 )
仮にバンドスペクトルを導入すると，その後，「バンドスペクトルは一見連続にみえるけれども，連続なものも，実はそうではない場合もあって，具体的には様々あって，LEDや蛍光体や分子やラジカルやプラズマの再結合や．．．．．」となりそうな気がします．  
　もちろん，学習が進んでいき，波動関数の混合などの段階になると，プラズマ中の分子スペクトルと蛍光体のスペクトルの共通性を学ぶことになるでしょう．決してそれを妨げているものではなく，初学導入段階において，将来とも矛盾ない方向性の提案ととらえていただければと思います．

     もし有機ELでエレクトロルミネッセンスが導入される以前であれば，「冷光」の用語を広める機会があったかもしれません．しかし，今やもう中学教科書にも有機ELがでてきているので，エレクトロルミネッセンスのほうを周知するほうが自然に思えます．

Q  白色LEDにはRGB３色のもあるが，それは確認されているか．
A   私の説明不足だったかもしれません．RGB３色のものは，輝度の点で現在，専ら装飾用につかわれるのみです．RGBの白色LEDは，CDの溝を通しただけでも，きれいに３色にわかれて観測できます．
ルミネッセンスという用語を使えば．
　3色RGBの白色LED :  波長の異なるエレクトロルミネッセンスの重ね合わせ
　青色LED+黄色蛍光体：青のエレクトロルミネッセンス（狭いもあもあ）と，その光によるフォトルミネッセンス（広いもあもあ）が重なったもの．
　と説明できるかと思います．

補足：スライドを作っていて，略語もあったほうが言いやすそうでした．
エレクトロ（電子/電界）ルミネッセンス：エレルミ
（カソード（加速電子/電子線）ルミネッセンスはエレルミといってもいいでしょう）
フォト（光）ルミネッセンス：フォトルミ
ケミ（カル）（化学）ルミネッセンス：ケミルミ
等．

レーザーについては，線幅が補足なりますが，
- 気体レーザー：気体放電中の輝線（電子衝突やペニング過程などの諸反応による）を共鳴増幅したもの
- 半導体レーザー（レーザーポインタ等）：エレルミの共鳴増幅
となるでしょうか．光ポンピングによるパルスレーザーの場合は，フォトルミの共鳴増幅です．
         （以上　2015.3.14）
========================
＜補足資料＞
上記の文献[1]は，アウトリーチに関する小特集（依頼記事）であり，概要執筆以降発行されました．ぜにご参照ください．ちなみに，物理学会の講演はプラズマの話題でありません（一般的な内容）．

プラズマ・核融合学会誌

小特集 社会との連携をめざしたプラズマ・核融合アウトリーチ活動の展開

（目次:タイトルからリンク有）

1.はじめに

2.理科教育の現場にプラズマ・核融合を   ← 上記文献[1]

3.高校生シンポジウムの取り組み

4.インターネットアウトリーチと核融合ポータル

5.「サン・ポール・レ・デュランスの風」への道のり

6.プラズマ・核融合学会広報委員会の取り組み

7.日本原子力研究開発機構のアウトリーチ活動の取り組み

8.核融合科学研究所のアウトリーチ活動の取り組み

9.プラズマ・核融合分野の社会連携について

- 小学校４年生の夏休み自由研究（親の視点で）-

- 小学校３年生の夏休み自由研究（親の視点で）-
http://plasmankado.blogspot.jp/2012/09/summer-homework.html [1]
を執筆して２年たった．続編を書こう書こうと思いつつ，１年過ぎてしまったが，昨年の夏休み，４年生の夏休み自由研究の状況について備忘録を兼ねて書く．

＜§1 テーマ選び＞

今回のテーマ選びはさほど苦労はしなかった．転校して住む場所が東京から京都に変わったので，変わった場所での「セミの抜け殻」を調べれば，「とりあえず」格好はつく．仮に昨年と同じような進め方になっても，場所がかわっているわけなので，学術論文でいうところの「重投稿」には該当しない(^^;)．先生も前年のものを知らない．

但し，全く同じ，というのは芸がないし，少しは成長したところをみたいものだ，という「親の淡い期待」もある．

めぼしい場所の検討はつけていたので，開始もやりやすいのだが，少し前年と状況は異なった．
-----------------------------
- １箇所にいる数が少ない．
- 近所に分散している
- したがって，前年のように，夕方と朝と続けてとり，１晩の分をすべて集める（１日分の数を調べる），ということが難しい． .... もちろん，これは親が判断^^
-----------------------------

東京の個体分布はミンミンゼミとアブラゼミで多くの場所ではアブラゼミが多いらしい．しかし鳴き声に関して言うと，ミンミンゼミの一人勝ちである．テレビドラマで使われるのも決まってミンミンゼミで，東京（？）の夏を象徴するといってもよいだろう． 一方，京都のセミの個体分布は主にクマゼミであり，特徴的なミンミンゼミの鳴き声が聞こえない．さらにニイニイゼミもいて，鳴き声にバラエティがある．そこで，本年度は鳴き声にも着目させたいと（親が）思った． 会話の中でその方向にどう誘導するかが問題．

＜§2 方法＞  -----  　　テーマ修正を納得させる．．．．

擬音語をつかっても，おそらく読み手には伝わらないだろう（しかし，このような観察も子どもにとっては大事なので取り組んでほしい）．まず音をよく聞く（観察ならぬ聴察）ことに重点を置きたい．

音声の解析と可視化には，最近流行しているスマートフォンのアプリに着目した．内蔵マイクからの音声をサンプリングし，それをフーリエ解析して周波数のスペクトルに変換する．人間が普段つかっている音域は当然，このマイクのサンプリング性能がカバーしているはずなので，好都合である．この周波数スペクトルがセミによってまったく違うことに気づいた（...もちろん専門分野では常識なのだろうが，私は初めて認識した）．それを子どもにみせると，（スペクトルの意味はわからなくても）視覚的に興味をもつようで，食いついてきた． ------>       「（私の心の声）よし，テーマ確定！（笑）」．

前年同様，A3のケント紙３枚（前年は４枚）を２つ折りにして，A4で12ページ分のブックレットにしたものを作成．ページ毎の配置を考える．

できれば，鳴き声（周波数）だけでうまく攻めたいのだが，本人の抜け殻へのこだわり（笑）があって，抜け殻の調査結果は必ず入れたいと譲らない（相変わらず誰に似たのか頑固である）．


そこで，「場所による違いを抜け殻で，時間による違いを鳴き声でやったらどうか」と持ちかけたら，乗ってきた（笑）．

＜§3 具体的作業〜ここからが本番〜＞


○場所の違い：
抜け殻を調べる．前年の作業を覚えているので，抜け殻あつめもスムーズだ．レポートでは簡単に昨年調べたことをレビューすることで定着も期待できるだろう．

いざ分類をやってみると，京都では大部分がクマゼミなので，場所によってあまり特徴的なことが言えない．

--------------------------------------------------------------------------
東京：　ミンミンゼミ ~ アブラゼミ >> ツクツクボウシ

京都：　クマゼミ >> アブラゼミ  >>  ニイニイゼミ, ツクツクボウシ（調査外の場所）
--------------------------------------------------------------------------

前年の研究がなければ，それでも形になったのかもしれないが，親の好奇心がそれを許さない（笑）．もっと詳しくしらべれば，ツクツクボウシなどの生息域もわかると思ったのだが，その調査が大変になることは（大人には）よくわかる．．．．ので，やんわりとその方向を避ける．．．

セミの抜け殻は具体的な「物」があるので，数を数えたり，分類したりした結果の整理が比較的容易である．しかし，鳴き声をどう表現するか．これはなかなか難しい（子どもにもよるだろうか）．時間帯によって主に聞こえる鳴き声も違うので，なにかこの音を小４の力量内で「可視化」できないか，と（親が）考えた．

○時間による違い：

　これは，大変おもしろかった．昼前にクマゼミの声がなくなり，やがて，ニイニイゼミの声が聞こえる．そして，アブラゼミが鳴き始める．聞いていても不思議であるが，周波数スペクトルにするとその違いがはっきりする．あとは，音とスペクトルを「子どもらしく」どう関連づけるかだろう．

 周波数とは「音が空気中をつたわる時，１秒間に何回空気が振動するか」と教えたら納得したようす．

そこで，聞いた音を文字で表現するのと，その音を周波数スペクトルで同時に表現するように書かせてみた．

----------------------------

　クマゼミ　　「ヴィヴィヴィ」　　　 2k-10kHzでモコモコしている

　ニイニイゼミ　「ヂー / 音程が時々下がってまた戻る」　6k-8kHzの間でピークがある．

    アブラゼミ「セリセリセリ」　　　　6kHzと14kHzに２つピークがある．
----------------------------

セミの鳴き声の周波数スペクトル

 周波数はスマートフォンの写真にセーブして，それをデジカメプリントで写真化したものを渡した．それを自分で切り貼りさせた．我が家はいまのところ，子どもにスマートフォンを持たせることには反対なので，このようにした．パソコンに取り込んで，それを印刷することもできたが，写真を自分で切り貼りしたほうが，与えられた，やってもらったという意識が小さくなると思ったからだ．

（ちなみに，ミンミンゼミの鳴き声の周波数帯域もクマゼミに近い．温暖化ともない，暑さに弱いミンミンゼミが北に追いやられている，という話も聞くが，この周波数の類似性によって両者が共存できない/しにくい，というこもあるのかもしれない．ミンミンゼミに「やつら（クマゼミ）耳障りじゃないか」聞いてみたいところ^^）

京都も山に登ると，ミンミンゼミの鳴き声が聞こえた（ヒグラシもいた）．絶滅ってわけではなさそうである．

＜§4 感想の書き方＞

いかに考察や感想を書けるかが，レポートの質を高める大きな要素になるのだが，我が子はそれがなかなか・・

感想を聞けば，「かしこいなあ」と思ったとのこと（この感想を引き出すだけでもひと苦労^^）．理由は「セミの仲間がどこにいるか分かりやすいから」．．　このあたりは何を想像してい表現しているのか思い知れないが，子どもらしいと言えば子どもらしい（笑）．

＜親の感想＞

自由研究にはいろいろな「ネタ本」が出版されているようだが，それを研究レポートの形に仕上げるにはなかなか子どもの独力では難しい．課題形式，質疑応答形式にすすめる必要がある段階だろう．個人差もあると思うが，独力での自由研究は，まだ小４でも尚早な気がする．

最近(2014.8)話題になった

「高校生の科学等に関する意識調査報告書-日本・米国・中国・韓国の比較-」
[ http://bit.ly/1voig8l ] の「概要=報道発表資料(PDF) 図21」によると，日本の子どもは他の三国に比べ，早期から自由研究をやっている．これは小中学校の夏休み課題として定着していることを意味しており，本来，創造性が発揮できるであろう高校以降に研究体験をする割合が圧倒的に少ない（リンク：http://twitpic.com/eam1n5）．

2014.8 高校生の科学等に関する意識調査報告書図20,21
 「自由研究」に関する日米中韓の比較... on Twitpic

現在，小学５年生での夏休み自由研究進行中である．例によって，夏休み終了直前，まだまだ完成にはほど遠い（笑）．５年生になり，やっと独力で作業できる段階にきているようだ．それでも独力で筋道をたてるには至っていない．もし独力で研究を成し遂げられるような教育を目指すなら，私見ではあるが，小学校高学年頃から少しずつ研究レポートの形式に慣れさせ，高校ぐらいでやや本格的なレポートが書けるような指導が適切な気がする．それまでは，親が助言を与えながら，科学の現象や用語に興味をもつこと，科学実験・観察へのアレルギーを無くすこと，文章に書くトレーニングをすること等に心がけてはどうかと思う．

以下小学校４年時の自由研究のスキャンPDFをアップする．ただし，人名，地名は伏せてある．
「＊＊にいるセミの鳴く時間に関する研究」
http://bit.ly/1nivhHw


小３編[1]で，「セミのぬけがらの研究」でのドタバタ劇を通じて「自由研究は，子供のため，というより，親が子供の全体的な達成度（＝現実：笑）を知るいい機会でもあるのかもしれない．」と書いたが，あらためてそう思った．

前年にくらべ，だいぶ筆が進むようになってきた．それなりに成長しているものだ（してもらわないとこまる）．しかしまだまだ「研究」っぽい内容を，自主的にテーマを選び自力で完成させていける段階には至っていない． ---- 逆に自主的にやるようになれば，おそらくこのような論評の機会もなくなるであろう^^.       (文責：plasmankado)
  

コピペ論文について

巷では理研小保方氏のSTAP細胞に関するNature論文における捏造，剽窃（コピペ）問題が世間を騒がせている．ひいては早稲田大学の学位論文審査の妥当性にまで飛び火している．

本稿では，かつて経験したコピペ論文の扱いを例に，思う所を述べたい．

＜論文審査システム＞
　卒業論文の審査は主査（例えば指導教員），副査（他研究室でその分野に精通してる教員），その他の審査員（その学科の教員全体）で為される場合が多いと思う．指導教員が主査になれない所も少なくないように，大学，学部によって相違はある．たとえば卒論が不要（卒業研究レポート，発表などで評価する）な大学・学部もある．博士学位論文では，学外の専門家に加わってもらうことも少なくない．

　正直，論文を隅々まで読むのは指導教員（主査）と副査までである．一般の審査員は，通常，概要集が事前配布されるが，論文本体は当日回覧であるところが多いように思う．
　そんなシステムのなか，，，

＜ことの起こり＞
　以前，ある論文（学部卒業論文）の副査にあたり，事前に配布された該当論文を読んでいた．すると奇妙なことに気づいた．研究の原理部分に記載された図が，数年前に私が指導した学生の修士論文に載せた図にソックリだったのだ．
　それで，過去の論文を引っ張り出してみると，その章の図だけでなく，16ページ中15ページにおよび文章まで同一であることがわかった．思い起こせば，その学生の先輩が，私の所で開発した手法を適用してみたい，ということで，元の修士論文のPDFを送ったことがあった（これはよくあること）．それが卒論生にわたっていると推測された．実際，論文の最後に参考文献として，その修士論文が挙げてあったが，当該箇所に引用はなかった．
　結果はさすがに当人の研究室の装置で得られたものであったが（そうでないと有無を言わせずアウト），原理手法の開発もオリジナルな研究である．同じ研究室の先輩の一子相伝の手法なら，100歩譲ってまだ理解できないわけでもない（当然それでもコピペ/丸写しは原則ダメ）が，他研究室で開発されたものを適切な引用なく，しかも文章を含め非常識な量コピペするのは明らかな御法度である．

＜審査会での対応＞
　審査会で，学生の発表後，副査が試問する．指導教員には（心の準備をしていただくため）事前にその旨を報告し，「私はこれを読んで怒っています．怒っている理由がわかりますか？」で試問を始めた．
　その時の学生の反応は，きょとんとしており，罪悪感がまったく見られなかった．なぜ私が怒っているか理解できなかったようである．

　罪悪感がないのは明らかである．なぜなら，「私」を副査候補として挙げるのは，学生本人であるからだ（もちろん指導教員とは相談する）．もし，後ろめたさがあったならば，審査で論文細部を読むことになる私は副査候補から外したであろう．そうしていれば，何事もなかったかのようにその場で卒論合格となった可能性も高い．原理部分なので，「教科書丸写し」の感覚だったのでは，と推測する．指導教員は必ずしもテーマ細部の専門とは限らず，しかも投稿論文ではなく修士論文であったので，これに気づくことが困難だったことは想像に難くない．（ 実は，その修論をまとめなおして英文化し，投稿論文にしようと考えていたが，忙しさにかまけてサボっていた負い目もある．．．．）

＜結末＞
　結果，（詳細経緯は機密であるが）審査会議で，その学生の卒論合否判定は保留となり，年度内卒業ができるギリギリの日程に，あらためて再審査を行うことになった．
　その経緯は私の研究室の修士論文と当該卒論とを見開き左右に配置し，上層部への報告書を提出した（ひと仕事だった）．
　再審査において，私は副査として，原理を表す図，および文章はコピペでなく，自分で作図，執筆するように要求した．研究者としては引用してもらうほうがいいのだろうが，本件は教育的指導のつもりだった（本人にそのメッセージが伝わったかどうかは正直わからない）．再審査の後，卒論は無事に合格となった．

　もちろん学者（の卵）であれば即アウトであるが，卒論はまだ研究のスタートラインでしかない．意図するしないにかかわらず，過ちも多々ある．研究者の卵として身を立てることができるかどうかをいわば採決する博士論文とは，やはり位置づけが異なる．このような”未遂”はけっこうあちこちで起きているのではないか，と推測する．同時に，すり抜けているものも．．．．本件，私を含めた審査員はその時点での判断として最善を尽くしたと思っている．

 　以降，卒論審査では卒論配属時に剽窃（コピペ）について厳しく警告する（すなわち即アウトとする）方針となった．

＜感想＞
　思い起こせば，その数年前頃より，レポート課題を出すと，立派だが似たり寄ったりのレポートが提出されることが気になりだしたように思える．こちらも対抗手段で．その文章を検索エンジンで検索し，オリジナルを探して，丸写しか咀嚼しているか考慮して採点するようなこともしていた（けっこうな労力であった）．
　そうして，私が課すレポートは調査よりも計算問題にすることが多くなっていった．同じ写すなら，コピペよりも友人のノートを書き写すほうがまだ力になると思ったからだ．加えて，レポートには「参考文献，ウェブサイトを明示すること．議論した友人があれば名前をあげ，謝意を示すこと．これは研究者としての最低限のマナーです」と添えるようにした．大学時代演習担当だった恩師のレポート課題（難題）の出し方に倣った．
　統計をとったわけではないが，謝辞に友人を挙げたレポートは徐々に少なくなり，個人がインターネットから探してくるほうが主流になってきたような気もする．

                                                                        ------ 以上，2014.4.24 執筆 (当時未公開)  -------

＜STAP騒動＞
   　上記の回想を書き記して，しばらくたった．「早稲田大学大学院先進理工学研究科における博士学位論文に関する調査委員会」が，小保方氏の学位論文についての所見を公表した
-------------------------
本研究科・本専攻における学位授与及び博士論 文合格決定にいたる過程の実態等を詳細に検討した上で、「上記問題箇所は学位授与 へ一定の影響を与えているものの、重要な影響を与えたとはいえないため、因果関係がない。」と認定した。
(http://www.waseda.jp/jp/news14/140717_committee.html)
-----------------------

　このような報告書の大変さは身に染みている（↑^^）
 　しかし，情報が多いと，かえって本質を見誤ってしまうのではないだろうか．

学位論文の審査は複数の研究者によってなされる．これが前提である．私を含め，研究者が論文を評価するときは，多かれ少なかれ，以下を基準とするはずである．難しい条件あれこれはもともと苦手な人達の集団である（．．よね？）．

(1) 序論
　これまでのその分野における背景を適切な引用のうえに紹介されているか．
　その中での自分の研究の位置づけが明確にされているか．
(2) 原理
　  オリジナルの場合には，一般的に再現，適用検証が可能なように書かれているか．
      オリジナルでない場合には，適切な引用がなされ，自分の言葉で説明されているか．
　 当該研究に則した改良，工夫点が明確に論述されているかどうか．
　（その際にも先駆者への配慮が適切になされるべきである）
(3) 結果
　　オリジナルな成果であるか（＝対象投稿論文の内容）．
　　論文の趣旨に「意味のある」データであるか．
　　自分の過去の投稿論文のデータであれば，それが明示してあるか．
　　（通常，他者の論文のデータは入る余地がない）
(4)  考察
　　結果をもとに合理的に書かれているかどうか．
　　先例があれば，それを支持する結果となっているか，あるいは反例となっているか．
　　（ここではもちろん他者の論文との比較等はあり得る）
(5)  総括
        この結果が当該分野に与えるインパクト，今後の展開など確固たる主張があるか．

このなかで，学位に該当する資質と業績があるかいなかは，(3)結果と(4)考察がすべてといって過言ではない．(1)序論や(2)（オリジナルでない場合の）原理は，審査前であれば，書き直させる指導ができる．しかし，結果や考察は，本人の数年間の蓄積であるので，本人の力量が試されるところ，さらに，だれもが経験するこの苦労は，自分で研究者としてやっていけるかどうかの洗礼でもあるだろう．
　この(3)で，証拠となるデータの信頼性がないのであれば，論外である．剽窃や捏造であれば即アウト．論文審査にあたる相応の専門家からみて，はたしてどうなのであろうか？これは審査員群の力量も試されるところであったはずである（のだが．．．．）．
　
　学位剥脱の是非判断は，（STAPの問題と先入観は切り離して）この点を中心になされるべきと思う．序論のコピペは（もちろんダメはダメで，審査すれば落第であるが），学位取り消し判定を左右するかといわれればまだ小さい（ルールに従えばアウトだが程度次第では温情の余地はあるという意  ---  本件は程度を越えてそうではあるが．．．）．
　極端にいえば，いったん学位を剥脱したとして，イントロを書き直せば，同じ論文で再審査して合格になる，ということは起こり得る．今回，こうする解もあると思う．それに対し，実験をやり直して，，，というのは到底あり得ない．

（推測であるが）芋づる式に，過去の他の学位論文の検証へと波及するのを恐れた「政治的判断」なのではないだろうか(朝日新聞記事参照)．内外で物議をかもしそうである．いずれにしても，この報告は学位取り消し判定についての大きな基準となるであろう．

　　　　　　　　　　　　　　　　　　　　　（2014.7.21  執筆：　7.26 迷いつつ公開）

(覚書　2014.4.10)
https://twitter.com/plasmankado/status/454197070832758784
https://twitter.com/plasmankado/status/454197248100810752
https://twitter.com/plasmankado/status/454197801212051456

＜学位取り消しの事例＞（ざっと調べた限り）
D(博士)
http://www.waseda.jp/jp/news13/131021_degree.html
http://www.u-tokyo.ac.jp/public/public01_220723_j.html
http://www.u-tokyo.ac.jp/public/public01_231209_j.html
http://www.kyushu-u.ac.jp/pressrelease/2009/2009-08-05-01.pdf
http://www.dokkyomed.ac.jp/dmu/news/20120827-1686.html
http://www.oita-u.ac.jp/01oshirase/gakuihenkan.html

M(修士)
http://www.jukushin.com/archives/10900
http://www.tsukuba.ac.jp/news/20111215160642.html

B(学士：卒論)
http://sfcclip.net/news2004090301 (awardの取り消し)



＜余談：論文審査＞
　以前，イタリアの工科大学の修士論文審査に呼ばれ（交換留学のような形式で私が日本での指導教員），出向いた時は，副査２名で，その副査からのコメントに対応した後，公聴会となる．公聴会には，親，親戚が聴きに来ることも多い（わけわからん発表でも子供の晴れ舞台，ということ）．公聴会の審査は，（当時）点数制ではなく，合議制であり，平常を見ている指導教員（主査と私）の意向が強かった．（ここまでは日本の審査に似ているが，このあとが面白く）点数は卒業式で一人づつ発表され，フルマーク（Maximum と言っていた, 学科で数名）だと拍手喝采で盛り上がる．私の弟子はフルマークをもらい，私の鼻も高かった^^．

　最近では，公平性という名の下，点数制（審査員全員で点数をつける）を採用するところも増えているように思うが，どちらも一長一短である．

　副査の選び方も様々であり，同じ分野の専門家が並ぶ場合もあるが，幅広い分野から審査される場合もある．たとえば，核融合プラズマ計測がテーマであれば，過半数をプラズマ実験の専門家が占める場合もあれば，プラズマ物理，核融合システム，エネルギープラント，光工学，データ解析，シュミュレーションの専門家で多角的に見る場合もある．指導教員は読んでいることが前提であろうが，副査の差（アタリハズレ？）は実際大きく，あまり読まずに要点だけかいつまんで，発表の際に試問する副査も少なくない．それが本質であったり，ど真ん中の専門家だと気づかない視点であったりもするので，一概に悪いとも言えないところが微妙である．

　無理なルール適用は，ルールに沿うこと自体が第一目的になってしまいがちである．私は，こと学術研究に関しては，あまり画一的に「こうあるべき」という型にはめない方が最適解に収まるような気がしている．
　　---- ただし，これは学術の性善説，自浄作用が前提にあることは確かである．．．．．．

フィギュアスケートジャンプ：人類は何回転まで到達できるのか？

■はじめに

　本稿のきっかけは職場のニュースレターへ「随想(page 8)」を寄稿するように依頼をうけ、フィギュアスケートに関して久しぶりに考えたことだった。原稿締切が２月初旬ソチオリンピックフィギュアスケート競技団体戦の真っ最中だったので，つい熱が入ってしまったが、3月末の発行時にはもうソチオリンピックも終わっているし、「随想」はページ制限があり（言いたいことを？）省略した内容もあるため、一部視点も変えてこのブログ記事に書き下すことにした。

　筆者は選手を引退してからもう15年近く（バッジテストは６級まで）になるが、最近の技術、プログラム構成の進歩はめざましい。団体戦での羽生選手の４回転トウループ、カウンターターンからのトリプルアクセルは絶品だった。さらに、2/14夜には男子シングルで羽生選手金メダル、町田選手５位入賞、高橋選手６位入賞にも感動した。今やほとんどの選手が４回転を入れたプログラム構成になっている。

　記録をさかのぼると、サルコウ選手の１回転サルコウジャンプ創始とされる1909年から２回転まで17年かかったが、３回転にはさらに29年、３回転から４回転には実に43年かかっている。いったい人類はいつ頃、何回転まで到達するのだろうか？

　本稿では、この自分自身の疑問に答えるべく、簡単な予想モデルを当てはめてみた。まずは結果をみていただきたい。

図１　国際スケート連盟(ISU)公式試合で４回転までの認定記録があるジャンプの予想。

いかにも「それらしい」モデル曲線になっている。　

　データ点は少なく、個人の技量の誤差もあるので、あくまで「シャレ」、というか「夢」というか、、、そのようなものだと思ってお読みいただきたいが、大変興味深い傾向がみえている。

■もちいたモデル式（数式アレルギーの方は読み飛ばしてください^^;）

　モデル式には、少ない係数で記述したい、という方針のもと、次式を採用した。

　y = A (1- exp( -( t - t₀) / τ )) . 

 この式のうち、エクスポネンシャル（指数関数）exp( )の中は時間t (> t₀ )が大きくなると0に近づく。どのくらいはやく近づくかというと、τ時間がたてば、「1/e」 (=約37%) になるペースである。したがって永久に0になることはない。この式は時間がたてばAに限りなく近づいていく、ということを意味する。

　つまり、人類の進歩は一定の割合で未知の限界に近づいていくという哲学（筆者の観念）を表している。

　「1/e； e分の1」のeはネイピア数といわれ、自然対数の底で2.718... という無理数である；高校の数学２−３年で学ぶ：理系だけ？

　（余談）仮に直線的に記録が伸びるなら、たとえば３０年ごとに１回転ずつ増えていく、ということを意味するが、誰が考えてもおかしいはずである。これまでにもマラソンや100m走の記録はxxxx年に女子が男子を抜く、とか、バタフライが自由形を抜くとか、そのような予想が有名科学雑誌に掲載されたり（引用は控える）、センセーショナルな報道になったり、まことしやかな情報として競技者に広まったりした。そこには、「肉体には限界がある」という概念が欠落しているように思っていた。実際に、上記のサルコウの記録をみても、回転数を１つ上げるのは並大抵のことではない。レベルはともかく選手経験があればごく当たりまえのことである。

　直線関係を仮定してみよう。直線を引くには２点のデータがあればいい（比例関係は原点をとおる直線関係であるので、比例であればデータ点が１つあればいい）。しかし、そこに３点目が加わると、「その直線で近似できるかどうか」、というのが問題となる。それが誤差評価である。直線が３点のどれにも近くなるように線を引くように小中学校（？）で学んだのを思い起こしていただきたい。この近似直線に対し、データ点のばらつきが大きければ、誤差が大きい、データ点がうまく乗っていれば誤差が小さい、と評価できる。

　直線は　y = ax + b なので、傾きaと切片bの値が決まると直線が確定する。このように、わかっているデータ点から係数a,bを求めることを、直線近似、あるいは直線フィッティングという。ここで難しいのは、現象は直線モデルで記述される保証はない、ということである。では、もう少し複雑な曲線だったらどうなるだろうか。

■データ点のモデル式（モデル曲線）へのあてはめ

　採用したモデル式はyとtを変数とする曲線で、その曲線を確定する係数は (τ, A, t₀ )の3つである。したがって、データ点が３つあれば、この直線が確定する。。。。かもしれない。　　

　なぜ、「かも知れない」、というかというと、このような係数が３元連立方程式の解としてすべて求まるとは限らないからである。どのくらいこの曲線に近いか、というのは別のもう１点以上が、この３つの係数できまるような曲線上にのっていることを確認しないといけない。

　つまり、４点あれば、「それらしい」曲線と、その誤差評価が可能となる。

そこで、データには、国際スケート連盟(ISU)公式試合で認定された４回転までの記録が現存する男子サルコウ、女子サルコウ、男子ルッツを用いた。

　

　採用したモデル式の「意味」は、西暦 t 年に y 回転に成功する（小数点も含む）ことを表し、Aは到達回転数限界、t₀は人類とジャンプ回転との格闘の仮想的な起点とみなせる。各ジャンプ記録データ４点がこのモデル曲線に乗るように係数 (τ, A, t₀ )を最小二乗法というもっとも一般的な解析手法で決定（関数フィッティング）すると、その後の進歩を予想する外挿曲線ができる。最も気になる係数はAで、Aの値が5を超えるなら5回転に到達するが、5より有意に小さい場合、到達不能と（筆者でなく）モデルが判定していることになる。

　ただし、回転不足ながら、認定を得る、という場合も無いわけではないので、それを考慮すると条件はかなり緩和される。

　τが大きいと、獲得するまでの期間が長く、逆にτが小さいと獲得が容易ということになる（筆者でなく、モデルがそう思ってる。。念のため。。）。

■フィッティング結果　(τ, A, t₀ )　

　男子サルコウ（64 ± 12, 4.96 ± 0.39, 1894 ± 2）、

　女子サルコウ（62 ± 3, 5.08 ± 0.12, 1906 ± 1)、

　男子ルッツ（53 ± 32, 4.48 ± 0.90, 1898 ± 9）-- 誤差が他より大きいことに注意。

　±の数字はフィッティングの誤差である。

■結果の解釈

　あらためてフィッティング結果（図１）を見ていただきたい。このモデルでフィッティングできたことだけでも少々驚きであった。

　係数Aは男子サルコウ4.96 ± 0.39回転、女子サルコウ5.08 ± 0.12回転、男子ルッツ4.48 ± 0.90回転であった。男女ともサルコウは22世紀頃に５回転に手がとどきそうである。対してルッツは、大きめの誤差範囲に5回転が含まれてはいるものの、データ点からかなりずれてしまう。よほど革新的な練習方法でも発見しない限り難しいように思う。現時点で４回転に未到達のループ、フリップも５回転は厳しそうである（もちろんあくまでモデル予測の話；若干の回転不足での認定まで含めると十分可能性はある---フアンとしては）。

　

　t₀のフィッティング結果も興味深い（偶然かも知れない）。

1896年第1回世界フィギュアスケート選手権（男子のみ）男子の t₀ がこのあたり。
1906年女子シングルのフィギュアスケート選手権で、女子サルコウの t₀ に一致。
　まさに、スケートジャンプとの格闘始まりに相応しい（国際スケート連盟は1892年設立とのこと）。

■このモデルの欠点（限界）

　 先に述べたように、個人の技量による誤差は少なくない。参考までに、全ジャンプの記録をプロットした図2を掲載する。　[ http://twitpic.com/7dnoat ]

図２　ISUで認定されたジャンプ初成功年。2011年現在。
分類のため、次のデータ点とは直線で結んである。

 図1で女子の可能性予測を押し上げているのは、2002年に世界初の女子４回転に成功した安藤美姫さん（誇らしいです）のデータ点。日本人の記録はもうひとり、1988年伊藤みどりさんが成功したトリプルアクセル（３回転半）があり、これはシングルからトリプルまでの３点をつなぐとほぼ直線になる。つまり、あっというまに４回転半に到達する、という予測になる。実際は、クワトラプルアクセル（４回転半）の成功年をデータに加えた時点で、予測モデルの係数が修正されることになる。

　男子トウループは２回転認定の記録がなく、４回転の出現が早い。仮に（少々乱暴であるが）t₀を1900年ぐらいに固定すると、実は今年にも５回転に到達するような予測曲線になる（いくらなんでも。。。。）。これも同様に、５回転トウループが出現した時点で係数、あるいはモデル自体を修正しなければならない。

　これらを無理矢理フィットすると図３のようになる。

図３　ある仮定をもとに推定した男子トウループと女子アクセルの回転数（仮）予想。

女子アクセルは３点を直線近似、トウループは起点を1900年に固定した本稿のモデル式。

これはあきらかに正しい予想とは言えない。

　明らかにこの予想カーブ（直線）は外れるでしょう。フィッティング結果からは、男子トウループは１８回転に向けて360年の時定数で近づいていくと出た（笑）。前述の陸上や水泳の予想と同レベルでしかない（「夢」といえば「夢」）。すなわち、予想はあくまでも予想で、モデルが妥当であることを、現実のデータから検証しながら用いていかないといけない。

　ただ言えることは、ほぼ間違いなく、トウループが最も早く５回転に達するであろうということだろう。

　個人の技量の誤差を緩和するには、例えば、第１０人目の成功年を採用する、最初の５人の成功年５点を使う、あるいは同一の選手権で３人が成功した年など、「神業」の域を脱した後のデータを調べ、モデルにあてはめてみるとよいであろう。ただ、現実的にはその記録を抽出するのは難しいのではないだろうか。

　

　技術革新について。練習法、指導法によって急にジャンプが跳べるようになる、というのは、選手であれば誰しも経験しているだろう。実際、ダブル時代のコーチがトリプルを、トリプル時代のコーチがクワトラプルを教え、成功に導いている。この技術革新も、回転数のデータ（歴史）にすでに組み込まれたものである（あった）のか、それとも、今後それがかわるのか、興味深いが予測するのは難しい。数学的には、時定数τの値が変化することになるが、データ数が限られる場合は予測モデルに入れることは不可能に近い。

■結果の考察

　図１から想像できるように、当分４回転まででの争いの時代が続くだろう。それに比べ図２で示されるように、あるジャンプの回転数が１つ上がる期間に比べると、その回転数の種類が増える期間は比較的短い。すなわち、いったんあるジャンプで回転数が上がると、その他の種類のジャンプもその回転数に達している。５種類の４回転ジャンプが出揃うのもそれほど遠い先ではないように思う（４回転半アクセルも）。

　ただし選手個人にとっては、師から弟子へ世代を超えながら回転数を上げていくのであるから、当然その修得は困難になる。加えて基礎力に相当するスケーティング技術や技の完成度も従来以上に要求されるので、基本に手を抜かずに効率的に圧縮して、早期に回転数を上げていくようなトレーニング方法論が必須となる。記録（図の点）にならない数多くの選手、コーチ達の努力が原動力となっていることも忘れてはならない。

（原案2014年2月7日、公開2月19日。文責：@plasmankado）

追記：==============================================
　2016年9月30日、羽生結弦選手が４回転ループを成功させた[スポニチ記事]。３回転ループの成功は1952年なので、実に64年ぶり。これで男子ループの点が４点になったので，予想曲線にフィティングさせた。結果を図４に示す。

図４　国際スケート連盟(ISU)公式試合で４回転までの認定記録があるジャンプの予想。
図1にループを加えた。男子ループの到達上限は4.27±0.10回転　

結果　(τ, A, t₀ )は

　男子ループ（43.7 ± 3.3, 4.27 ± 0.10, 1898 ± 1）
となった。この4.27回転という数字が、人類の限界を表す。（あくまでこのモデルに従うと）誤差を考慮しても、また多少の回転不足でも認定されることもあることを考慮しても、やはり５回転は難しい、ということなのかもしれない。
　とすれば、練習方法や助走フォームなどの進歩ももちろんであるが、他のスポーツ同様、フィギュアスケート界も、スケート靴やブレード等の画期的な技術革新を望んでもいい時期なのかもしれない。

　実は2016年の4月に宇野昌磨選手が４回転フリップを成功させている（誇らしいですね）。ただ，男子フリップの成功年記録が１回転と４回転しかないため、予想曲線を引くことができない。

（2016年10月1日。文責：@plasmankado）

補足：

-　シングル、ダブル、トリプルまでは馴染みがありますが、４回転以上はどういうのでしょうか。

　4回転：クワドラプル(quadruple),  5回転：クインタプル(quintuple) と続きます[wiki]。

-　ジャンプには整数回回転５種類（現行ルールの基礎点が低い順にトウループ、サルコウ、ループ、フリップ、ルッツ）と半整数回回転１種類（アクセル）がある [フィギュアスケートの採点法]。回転数が少ないと、トウループよりサルコウのほうが容易な印象であるが、回転数が上がると、助走の回転とトウの反発力を直接接続できるトウループのほうが若干やさしい、という評価のようだ（同意）。

　　　　　

参考：

　寄稿したニュースレター：No.54(2014年3月)発行予定
       → 3月31日発行(pdf版)。第8ページ「随想: フィギュアスケートジャンプは何回転まで到達できるのか?」。

　基礎学力の早期充実について一考。「スペシャルジャンプだけでは(PDF)」(淡青評論 No.1371 2008年3月14日p.44 裏表紙)